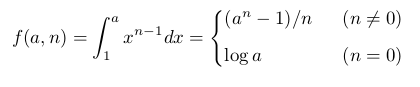xn-1 fonksiyonunun türevi her n için tanımlı. Ama iş türevin tersine gelince, 1/x için belirsiz integral beklenmedik şekilde logaritma çıkıyor. Acaba neden n=0 farklı bir rejim? Bu farklı davranış xn fonksiyonundan türetilebilir mi?
xn-1 fonksiyonunun 1'den herhangi bir pozitif a sayısına kadar integrali için iki farklı formül var:
f(a, n) n'nin sürekli bir fonksiyonu ise, n parametresi sıfıra yaklaşırken iki ifadenin eşit olması gerekir:
İkinci örneğimiz analitik geometriden:
y² = 1 + ax² y ≥ 0, −1 ≤ x≤ 0
fonksiyonu a>0 için hiperbol, a<0 için elips tanımlar.
a=0 durumunda konik yerine y=1 doğrusu çıkar.
Peki, a sıfıra (her iki yönden) yaklaşırken ne olur?
Küçük x değerleri için, yaklaşık olarak bir parabol bulduk.
Üçüncü örnek basit bir diferansiyel denklem: y' + y = e-kt, y(0) = 8
Bu denklemi sağlayan y(t) fonksiyonu için iki ayrı çözüm şekli var:
a) k = 1 ise çözüm üstel fonksiyonun lineer bir ifade ile çarpımı:
y(t) = e-t (8 + t)
b) k = 1 değilse çözüm iki farklı üstel fonksiyonun toplamı:
y(t) = A e-t + B e-kt
Çok farklı iki ifade bulduk ama k parametresi 1'e yaklaşırken iki çözümün yaklaşık eşit olması gerekir. Mesela k = 1.01 için, A ve B katsayıları denklemden ve başlangıç şartından bulunabilir:
y(t) = 108 e-t − 100 e-1.01t
Bu ifade şöyle yazılırsa (a) çözümüne yakın olduğu görülür:
y(t) = 8 e-t + 100 e-t (1 − e-0.01t)
Burada e-0.01t yerine yaklaşık değeri olan 1 − 0.01t koyunca yukarıdaki (a) çözümüne hemen ulaşılır.
Aynı sonuç, e-xt fonksiyonunun x = 1 noktasındaki türevi olarak da bulunabilir. Yani e-xt fonksiyonunun t'ye göre türevinden başlayıp aynı fonksiyonun x'e göre türevine ulaşmış olduk.
Ödev
1. ax² − 4x + 20 = 0 denkleminin a≠0 için çözümlerinden birinin, a sıfıra yaklaşırken 5 değerine yaklaştığını gösterin
2. c parametresine bağlı olarak şu denklemin üç ayrı çözüm şekli var:
y'' + 2y' + cy = 0, y(0) = 2, y'(0) = 0
a) c=1.00 ise y(t) = 2 e-t (1 + t)
b) c=0.99 ise y(t) = 11 e-0.9t − 9 e-1.1t
c) c=1.01 ise y(t) = 2 e-t (cos 0.1t + 10 sin 0.1t)
(b) ve (c)deki iki farklı fonksiyonun t≪1 için (a) fonksiyonuna yaklaştığını gösterin
Referans
Bu yazının aslı, birkaç ay önce Damlalar: Süreklilik olarak yayınlanmıştı